ShortestDistance

Description

This operation computes the shortest distance from the initial state to every state (when reverse is false) or from every state to the final states (when reverse is true). The shortest distance from p to q is the ⊕-sum of the weights of all the paths between p and q.

The weights must be right (left) distributive if reverse is false (true) and k -closed (i.e., 1 ⊕ x ⊕ x ² ⊕ ... ⊕ x ^{k +1} = 1 ⊕ x ⊕ x ² ⊕ ... ⊕ x ^k ) (valid for non-negative TropicalWeight) or k -closed when restricted to the automaton (valid for TropicalWeight with no negative weight cycles).

Usage

template<class Arc>
void ShortestDistance(const Fst<Arc> &fst, vector<typename Arc::Weight> *distance, bool reverse = false);

fstshortestdistance [--opts] a.fst [distance.txt]
    --reverse: type = bool, default = false
      Perform in the reverse direction

Examples

A, over the tropical semiring:

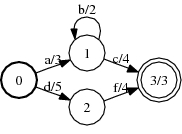
(TropicalWeight)

Shortest distance from the initial state

ShortestDistance(A, &distance);
fstshortestdistance a.fst

Shortest distance to the final states

ShortestDistance(A, &distance, true);
fstshortestdistance --reverse A.fst

Complexity

ShortestDistance:

• TIme:
  • Acyclic: O(V + E)
  • Cyclic:
    • Tropical semiring: O(V log V + E)
    • General: exponential
• Space: O(V)

Caveats

See here for a discussion on efficient usage.

See Also

ShortestPath, State Queues

References

• Mehryar Mohri. Semiring Framework and Algorithms for Shortest-Distance Problems, Journal of Automata, Languages and Combinatorics, 7(3):321-350, 2002.

-- CyrilAllauzen - 05 Jul 2007