Minimize
Description
This operation performs the minimization of deterministic weighted automata and transducers.
If the input FST
A is an automaton (acceptor), this operation produces the minimal automaton
B equivalent to
A, i.e. the automata with a minimal number of states
that is equivalent to
A.
If the input FST
A is a transducer, this operation internally builds an equivalent transducer with a minimal number of states. However, this minimality is obtained by allowing transition having strings of symbols as output labels, this known in the litterature as a
real-time transducer. Such transducers are not directly supported by the library. By defaut,
Minimize will convert such transducer by expanding each string-labeled transition into a sequence of transitions. This will results in the creation of new states, hence losing the minimality property. If a second output argument is given to
Minimize, then the first output
B will be the minimal real-time transducer with each strings that is the output label of a transition being mapped to a new output symbol, the second output transducer
C represents the mapping between new output labels and old output labels. Hence, we will have that
A is equivalent to
B o C.
Usage
template<class Arc>
void Minimize(MutableFst<Arc> *fst, MutableFst<Arc> *sfst = nullptr, float delta = kDelta, bool allow_nondet = false);
|
fstminimize in.fst [out1.fst [out2.fst]]
|
Examples
Acceptor minimization
A |
B |
 |
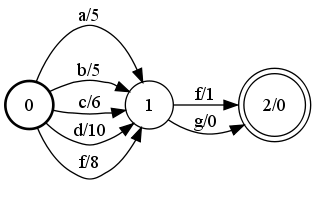 |
Minimize(A, &B);
fstminimize a.fst b.fst
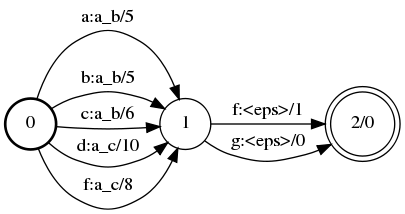
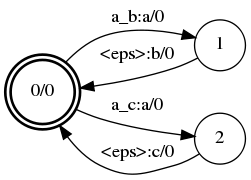
Transducer minimization
A |
B |
 |
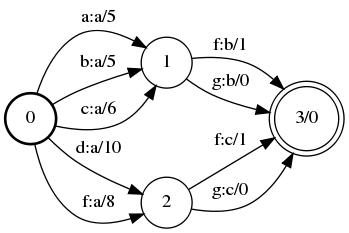 |
Minimize(A, &B);
fstminimize a.fst b.fst
Minimize(A, &B, &C);
fstminimize a.fst b.fst c.fst
Complexity
Minimize
- Time:
- Acyclic: O(E)
- Unweighted: O(E log V)
- Weighted: complexity of shortest distance + complexity of unweighted minimization
where
V = # of states and
E = # of transitions in the input Fst.
References
- John E. Hopcroft. An n log n algorithm for minimizing the states in a finite automaton. In Z. Kohavi, editor, The Theory of Machines and Computations, pages 189-196. Academic Press, 1971.
- Mehryar Mohri. Minimization algorithms for sequential transducers
 . Theoretical Computer Science, 234(1-2): 177-201, 2000.
. Theoretical Computer Science, 234(1-2): 177-201, 2000.
- Dominique Revuz. Minimisation of Acyclic Deterministic Automata in Linear Time. Theoretical Computer Science, 92(1): 181-189, 1992.





 . Theoretical Computer Science, 234(1-2): 177-201, 2000.
. Theoretical Computer Science, 234(1-2): 177-201, 2000.

